Particle transport in non-Newtonian fluids

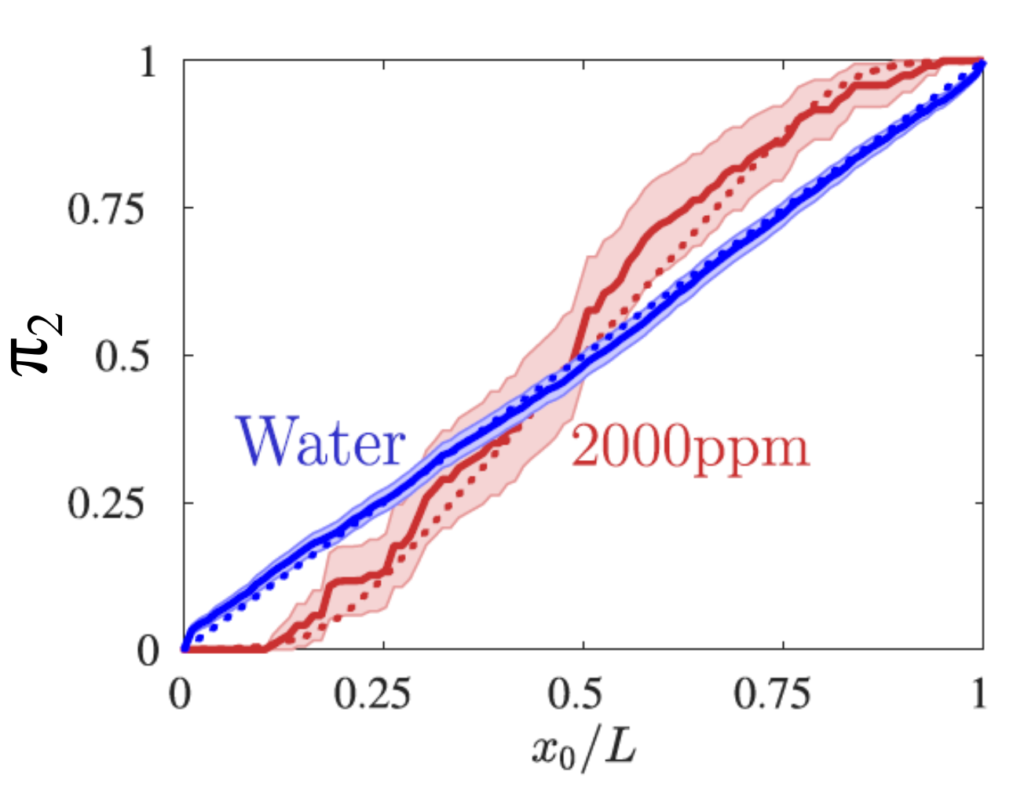
Splitting probabilities quantify the outcome of competitive events. Determining splitting probabilities is fundamental in random walk theory. The statistics of competitive events is well understood for memoryless (Markovian) processes. However, in complex systems such as polymer fluids, the motion of a particle is typically described as a process with memory. The behavior of viscoelastic fluids differs from that of simple Newtonian media due to their distinct microscopic organization, typically involving the presence of macromolecules or nanostructures which are obstacles for the particle motion.
Here, we designed an experiment in which Brownian particles diffuse in a viscoelastic solution (PAM). A dark-field microscope was used to obtain a long time particle trajectory with high spatiotemporal resultion. The experimental data agrees well with the splitting probabilities for general non-Markov processes.
Collaborators: Toni V. Mendes(Univ. Bordeaux); Hamid Kellay (Univ. Bordeaux); Thomas Guérin (CNRS, Bordeaux)
Paper: Evidence and quantification of memory effects in competitive first passage events. arXiv:2402.05005v1
